Voor ik mij erin verdiept had, leek het erop dat het instellen / aanbrengen van de ‘relief’ (hol maken van de toets) de snaarafstand vergrootte in plaats van die te verkleinen. Het principe hierachter werd me pas duidelijk na het lezen van een artikel, waarin meetkundig wordt bepaald hoe de optimale holle (concave) toets eruit dient te zien. Het artikel was geschreven door gitaarbouwer en gitaarbouwdocent Oswald Verbeij. Ik zal hier met zijn toestemming enkele citaten en conclusies delen.

Met de tekening wordt het principe verduidelijkt. De verticale schaal is 50x vergroot: dit is gedaan omdat relief een kwestie van tiende millimeters is, en bij een 1:1 schaal de lijnen niet te onderscheiden zouden zijn. Wel heeft deze vergroting in één dimensie allerlei vervormingen tot gevolg: sinussen zijn niet meer symmetrisch, haakse hoeken zijn geen 90⁰ meer en gelijke snaarhoeken zijn verschillend. Ter verduidelijking daaronder dezelfde tekening, maar dan met de snaren ter hoogte van fret 7, 8 en 9 zowel horizontaal als verticaal uitvergroot, zodat te zien is dat in de praktijk met hoeken van 90⁰ gerekend mag worden.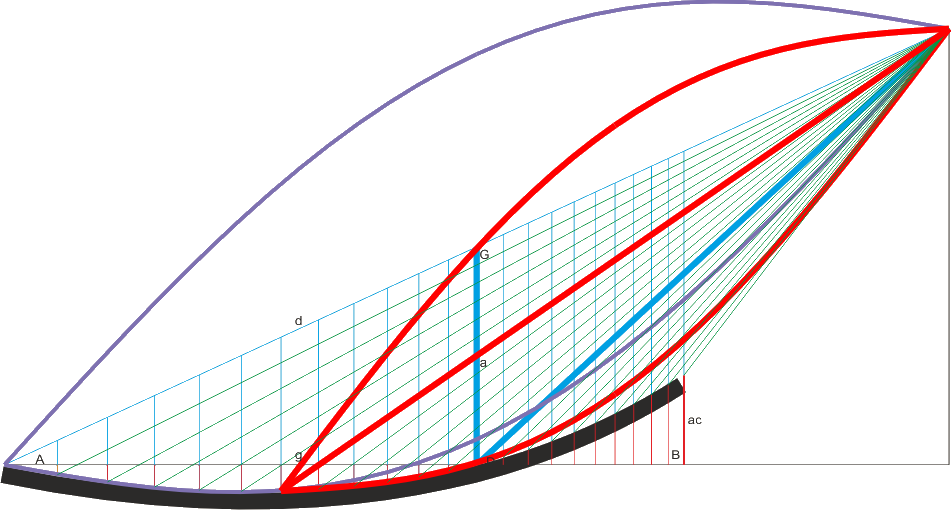

Toets, snaren en max amplitudes (losse snaar en gefret op pos. 6)

Het principe bestaat hieruit dat de hoeken die de ingedrukte snaren op opeenvolgende posities onderling en met de toets vormen steeds gelijk zijn; dit kan alleen bereikt worden door de toets hol te maken. Het is te zien hoe beide de voluit trillende snaren, de losse (paars) en de op fret zes ingedrukte snaar (rood), ca. 6 frets lang netjes de toets volgen. Omdat alle driehoeken gelijkvormig zijn, geldt dit voor alle fretposities.

Bij een vlakke toets is de ruimte tussen de gefrette snaar en de opvolgende frets constant over de gehele lengte (de hoek wordt groter, maar de afstand tussen de frets neemt evenredig af, waardoor bij een ingedrukte snaar de snaarhoogte bij de volgende frets steeds overal op de toets gelijk is). Bij een goedgevormde holle toets, is de relatieve snaarhoogte bij elke fretpositie identiek (dus: minder snaarlengte = evenredig kleinere amplitude = evenredig geringere snaarhoogte). De berekeningen hoeven dus ook niet voor alle mogelijke gefrette snaarposities herhaald te worden, maar gelden overal: slechts de waardes veranderen, maar niet de verhoudingen.

De spreadsheet waarmee de kromming wordt berekend kun je downloaden via deze downloadlink. De materie is vrij complex en heeft me moeite gekost het te begrijpen en in de spreadsheet samen te vatten.

Voor de volhouder die de spreadsheet evt. downloadt: De laatste twee kolommen dienen om in de praktijk met een rei de snaarhoogte bij een bas te controleren tot fret 12 of 19 bij een actie van 3.5 mm. Uiteraard kan een andere actie worden gekozen, waardoor de getallen zullen veranderen. De nulniveaus in de kolommen geven aan op welke frets de rei moet rusten (kan uiteraard zonder rei: capo op fret 1, op andere fret met vinger snaar indrukken en snaarhoogte meten).

Conclusies (referentielat rustend op fret 1 en 12):

• De optimale toets is lichtelijk concaaf, met een positieve relief van 1/10 van de snaaractie (bij fret 6).
• De optimale topkamhoogte is 1/20 van de snaaractie.
• Ervan uitgaande dat de toets de optimale relief heeft gekregen, geldt bij de basgitaar dat bij gelijk blijvende actie, de maximale amplitude 37% hoger is dan met een vlakke toets! (3,07/2,24 = 1,37).
• De optimale toets moet in de hogere regionen (boven fret 12) blijven oplopen (vergeleken met de referentielat).
• Zowel relief als topkamhoogte zijn onafhankelijk van de mensuur, alleen de actie is bepalend!

De praktische voordelen:

• Sterk verlaagde actie: omdat zoals vermeld de actie (bij fret 12) 37% lager kan worden door de juiste kromming te gebruiken, neemt ook de snaarhoogte hoger op de toets sterk af: een actie van 3,5 mm bij fret 12 bij een rechte toets, staat gelijk aan een actie van 2,24 mm bij het gebruik van een optimaal gebogen toets.
• De afstand tussen snaren en frets loopt bij een rechte toets steeds verder uiteen, terwijl bij een concave toets de toename steeds minder wordt.
• Geen backstring buzzing meer (Het aanlopen van snaren achter de fretvinger). De eventueel mee-resonerende stukken snaar lopen vanwege de holle toets niet meer aan, en produceren dus geen geratel meer.

Opmerking:
De fout die veroorzaakt wordt door mensuur gelijk te stellen aan de snaarlengte valt binnen de foutmarges, gezien het feit dat (volgens Pythagoras) geldt:  =  = 650,03 mm.